Carbon Dating: How Radioactive Isotopes Estimate Age

What is carbon dating?

Since the discovery of carbon dating, it has revolutionized our understanding of our planet. For example, we can finally put a date on prehistoric life forms and rock strata.

By understanding how old things are, we can organize events in chronological order. Not only do archaeologists use carbon dating for excavated artifacts, but geologists use it for stratigraphy.

Now that you have a basic understanding, let’s get into the details of how carbon dating works.

“Carbon dating reveals the age of fossils by measuring radiocarbon. Carbon dating measures the ratio between two naturally occurring types of carbon – carbon-12 and carbon-14.”

How carbon dating estimates age

Carbon dating considers two naturally occurring types of carbon on Earth:

Carbon-12 (C12) is stable with 6 protons and 6 neutrons.
Carbon-14 (C14) is a radioactive isotope with 6 protons and 8 neutrons.

Living organisms are constantly taking in carbon-12 and carbon-14. In fact, the types of carbon in our bodies correlate with the amount of carbon-12 and carbon-14 in the atmosphere.

If you look at our atmosphere, about 99% of carbon is carbon-12. But there are only trace amounts of carbon-14. And the amount of C14 in any living thing is pretty consistent.

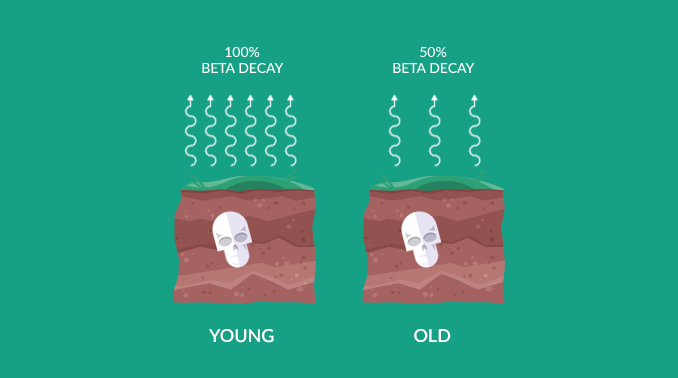
“When an organism dies, carbon-14 drops at a predictable rate. After 5,730 years, it contains half the carbon-14 as it did when it was alive. So, it has a half-life of 5,730±40 years.”

How does the ratio of carbon-14 to carbon-12 determine age?

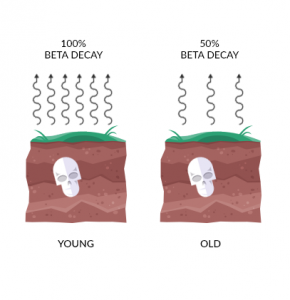
When an organism dies, it ceases to take in carbon from the atmosphere. So right before it dies, it starts with the same amount of carbon-12 and carbon-14 in the atmosphere at the time. This is why we look at the ratio between C14 and C12.

If the atmosphere had a C14/C12 of 0.01%, then a C14/C12 of 0.005% means it died about 5,730 years ago. This is because carbon-14 decays into nitrogen-14 with a half-life of 5,730±40 years.

Then, at 11,460 years old carbon-14 would go down to 0.0025%. All throughout, carbon-12 in the fossil records stays constant. But every 5,730 years, half of the carbon-14 decays.

“In summary, when you take a sample from a fossil, carbon-12 remains fixed. But carbon-14 decays predictably over time. By examining the ratio between the two for dead matter, we can estimate age.”

What are the limitations of carbon dating?

Despite the revolutionary impact that carbon dating has given to date organic matter, it has its limitations. For example, it needs enough carbon-14 remaining in an organism to make an accurate estimate.

At a certain age (60,000 years or so), there isn’t enough carbon-14 to reliably put a date on prehistoric life. In addition, we can only use carbon dating on organic matter. Whereas materials such as metals cannot be carbon-dated.

Finally, we know that the interaction between cosmic radiation and CO₂ creates carbon-14. But it’s difficult to put an exact number on how much carbon-14 was in the atmosphere when it died.

If you look at Earth’s atmospheric history, its composition has changed significantly over time. But scientists have their ways to figure it out.